Introduction
Filters are a very powerful tool when it comes to building the character of your sound, they allow some frequencies to pass and attenuate others, depending on what kind of filter you’re using, they can be subtle or completely modify your sound. There are many possible filter designs - a filter is an amplifier whose gain changes with frequency and that can be used in several ways. Think about it, a lot of effects we use are filter effects.
A delay network can have a gain that varies as a function of frequency and a delay network that is designed specifically for its frequency or phase response is called a filter (PUCKETTE, 2007). We’re going to take a look at that specific type of filtering.
A little heads up here: I will introduce some concepts before we get to the patching but please don’t run away, I promise we’ll get there (or just skip over if you feel like it). A comb filter is a Linear Time-Invariant (LTI) filter implemented by adding delay to the original signal creating amplifications and cancellations to the waveform. However, you can also implement time varying comb filters to produce some greatly used effects such as phasers, flangers and chorus.
Let’s break it down
Linear time-invariant means:
- linear: the output is linearly related to the input.
- time invariant: it doesn’t matter when an input was applied, its behavior will be the same
LTI filters are characterized by their impulse response, so any LTI filter can be implemented by convolving the input signal with the filter impulse response. We’ll take a look at our patches impulse responses soon.
We have two basic types of comb filter: feedforward and feedback, referring to the direction in which signals are delayed before they are added to the input.
FEEDFORWARD
The feedforward comb filter is a particular type of finite impulse response (FIR) filter, in other words, the impulse response is of finite duration, because it settles to zero in finite time - you’ll see in the demonstration video that as soon as I shut it down it stops. In this type of filter the output is a linear combination of the direct and delayed signal.
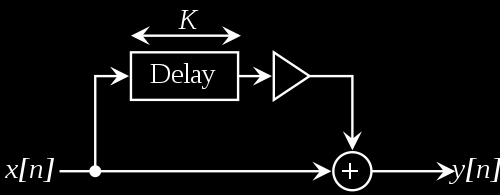Fig. 1 - Feedforward comb filter structure by Krishnavedala / CC0
Let’s test this with Pd and then analyze the response. I’m going to feed an impulse that is going directly into the output and writing a copy of it to [delwrite~] that will be added into the signal before the output.
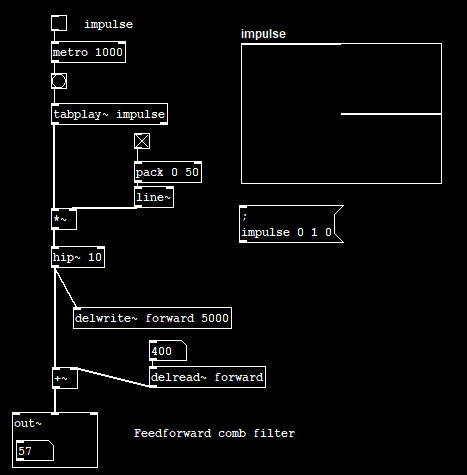Fig. 2 - Feedforward comb filter implementation in Pd
Feedforward comb filter demonstration
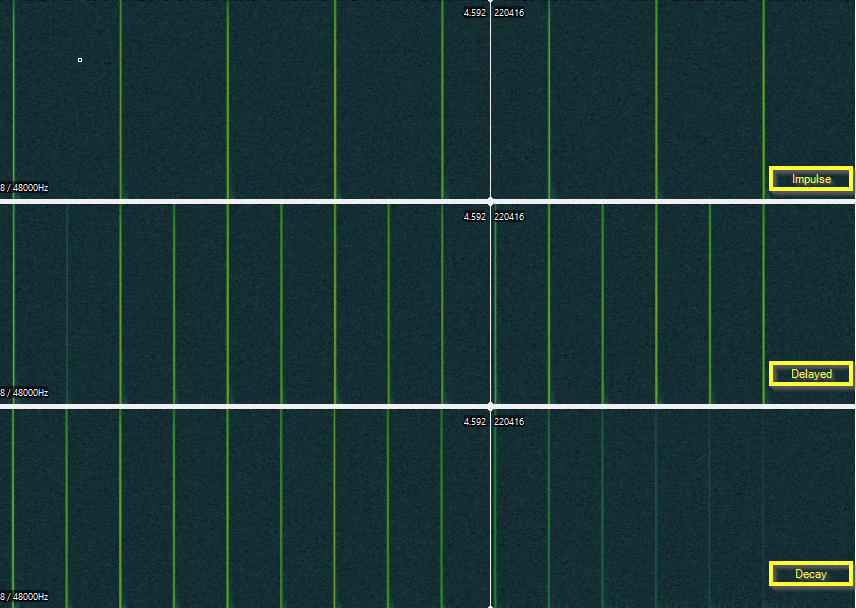
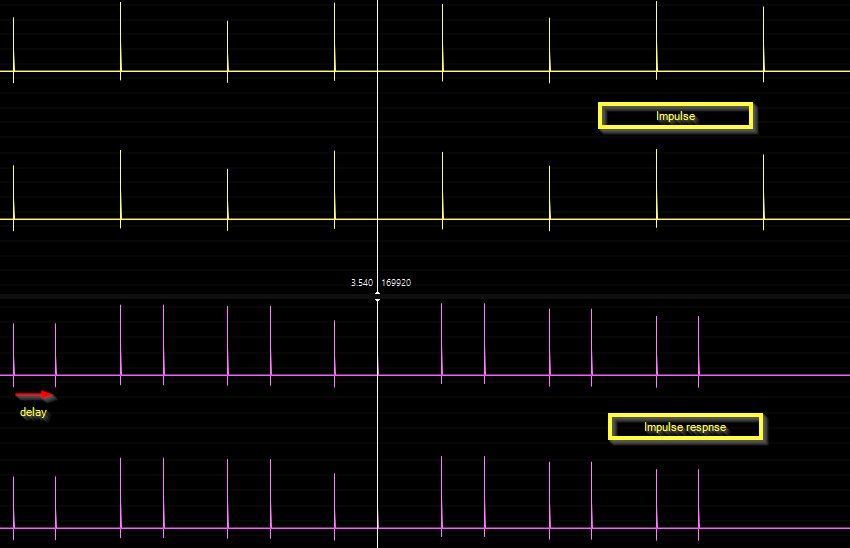Fig.3 - Impulse response of a non-recirculating (feedforward) comb filter
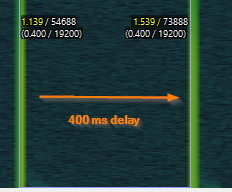Fig.4 - Amount of delay being read as defined in [delread~]
FEEDBACK
The feedback comb filter has an Infinite Impulse Response (IIR), that happens because there is feedback from the delayed output being fed to the input so it continues indefinitely as a repeating series of impulses of exponentially decaying amplitude over time. In the video demonstrations you’ll see a different behavior from our previous patch.
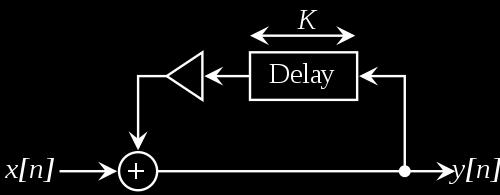Fig. 5 - Feedback comb filter structure by Krishnavedala / CC0
In Pd, I created an array consisting of a simple signal for testing and played it back using [tabplay~], that signal is sent down a delay line and the delay lenght is defined in ms [delwrite~ fbcomb 5000]. [delread~ fbcomb] is the delay line output, we have to multiply it by a gain before being fed into the input. Be careful when multiplying because if you multiply by a number greater than 1 or less than -1, instead of an exponential decay the signal will keep adding up and growing creating an unstable system.
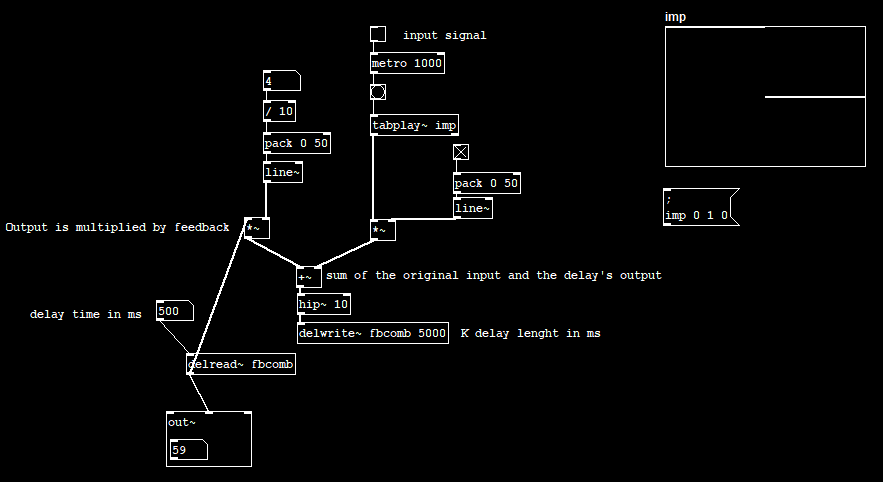Fig. 6 - Feedback comb filter implementation in Pd
Feedback comb filter demonstration
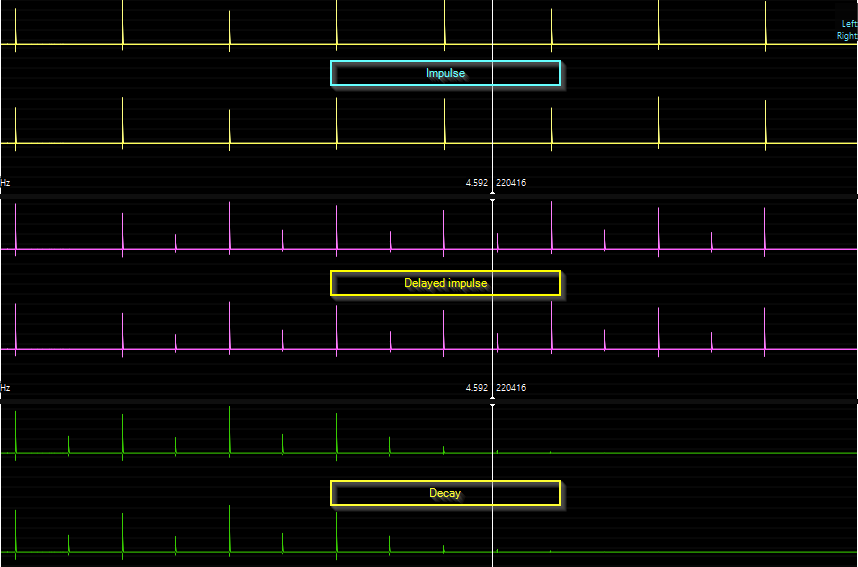Fig.7 - Time domain behavior of the delay network
Fig.8 - Spectrogram analysis
Comb filtering can occur as an undesirable result of reflections in your studio or be used intentionally as a creative tool. Understanding how it works can be helpful in fixing or creating things. Once again, if you want to learn more and understand the subject more deeply, I strongly recommend the material in the references section.
References
Puckette, Miller. The theory and technique of electronic music. World Scientific Publishing Company, 2007.
Russ, Martin. Sound synthesis and sampling. Taylor & Francis, 2004.
Github repository (patches here):
https://github.com/nico-audio/pd-patches
Julius Orion Smith III website pages:
https://ccrma.stanford.edu/~jos/filters/What_Filter.html
https://ccrma.stanford.edu/~jos/filters/Impulse_Response_Representation.html
https://ccrma.stanford.edu/~jos/pasp/Comb_Filters.html
Wikipedia Comb Filter page: https://en.wikipedia.org/wiki/Comb_filter